优化

Optimization

“一般来说，优化问题都是不可解的”。—— Yurii Nesterrov

在给定的约束条件下，寻找一个或多个变量的值，以最大化或最小化一个目标函数

优化变量
目标函数 (Objective Function): 需要优化（最大化或最小化）的函数。
约束条件 (Constraints): 决策变量必须满足的条件。

单目标优化（最大化，最小化），多目标优化

数值方法
解析方法

最优是对于特定指标的最优

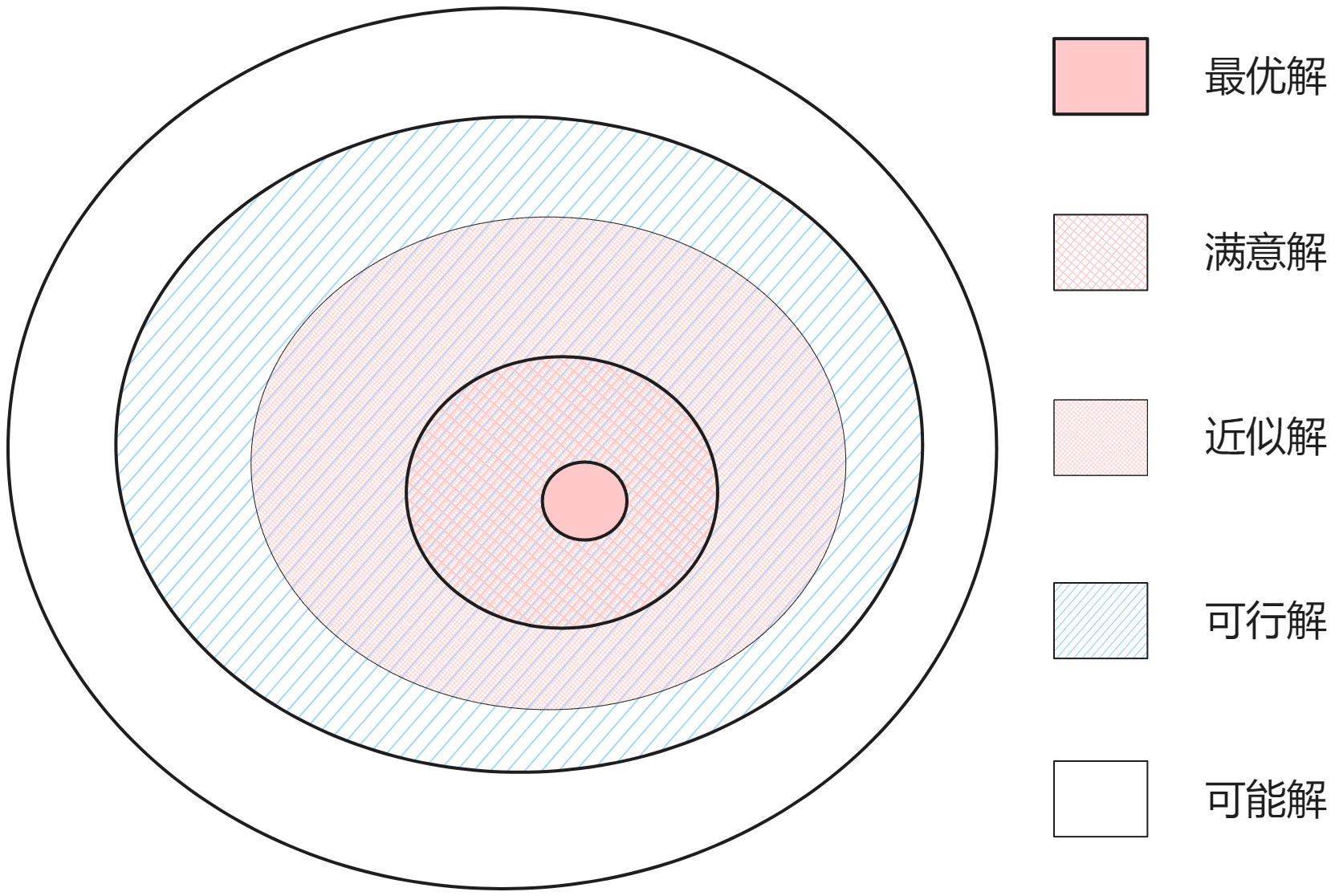
解的类型

可行解 (Feasible Solution): 满足所有约束条件的解。
最优解 (Optimal Solution): 使得目标函数达到最优的可行解。

基本流程

凸优化

Convex Optimization
数学优化领域中的一个重要分支，它研究的目标是求解凸函数在凸集上的最小化问题。
凸集 (Convex Set): 如果集合中的任意两点之间的线段完全包含在该集合内，则该集合是凸的。
凸函数 (Convex Function):
对于任意两点 $x, y$ 和任意 $λ \in [0, 1]$ 都有

\begin{array}{r} f (λ x + (1 - λ) y) \leq λ f (x) + (1 - λ) f (y) \end{array}

则 $f$ 为凸函数
凸优化问题通常比一般的非凸优化问题更容易求解，因为凸优化问题通常保证有全局最优解，而且存在有效的算法来找到这个解。此外，凸优化问题在理论上也更加丰富，因为它们满足许多优美的数学性质。

常见算法

线性规划

最优控制
 群智能优化算法
 并行计算 (Parallel Computing): 利用多核和分布式计算资源来加速优化过程
机器学习与优化 (Machine Learning and Optimization): 结合机器学习技术来改进优化算法的自适应性和鲁棒性

解析方法 (Analytical Methods): 如拉格朗日乘数法（Lagrange Multipliers）用于求解带等式约束的优化问题

数值方法 (Numerical Methods):
如梯度下降法（Gradient Descent）
牛顿法（Newton's Method）

梯度下降法（Gradient Descent）
线性规划（Linear Programming）
非线性规划（Nonlinear Programming）